Topológia-megőrző redukciók a $\sc T$ mozaikon
Ezen az oldalon az egyszerűség jellemzésére ill. a redukciók topológiai korrektségének vizsgálatára vonatkozó azon, általunk javasolt kritériumokat fogalom össze, amelyek a $\sc T$ mozaikon mintavételezett képeket feltételeznek.
Egyszerű pixelek jellemzése
4. Tétel: [7] A $({\sc T},k,\ov{k},B)$ képnek $((k,\ov {k}) = (2,1), (1,2))$ egy $p ∈ B$ pixele akkor és csakis akkor egyszerű, ha az alábbi feltételek teljesülnek:
- $p$ pontosan egy $N^{*V}_k(p)∩ B$ halmazbeli $k$-komponenssel $k$-szomszédos.
- $p$ pontosan egy $N^{V}_k(p) ∖ B$ halmazbeli $\ov{k}$-komponenssel $\ov{k}$-szomszédos.
Megfigyelhető, hogy az 1. tétel 2. és 3. feltételei a figyelembevett szomszédsági relációk típusától eltekintve rendre megegyeznek a 3. tétel 1.\ és 2.\ feltételével. Fontos azonban kihangsúlyozni a két tétel közötti alapvető különbséget: az előbbi szerint a $p$ pixel egyszerűsége az említett feltételek egyike alapján is eldönthető, míg utóbbi esetben ehhez mindkét kritériumra szükség van.
A Kong által bevezetett "csatolt halmaz'' fogalma könnyen kiterjeszthető úgy, hogy az a $\sc T$ mozaikra is érvényes legyen: ebben az esetben a csatolt halmaz a pixelt határoló háromszög éleinek és csúcsainak részhalmaza alkotja a csatolt halmazt. Ebből a fogalomból kiindulva $T$ mozaikon egy további hasonló összefüggés bizonyítható, mint négyzetmozaik esetén.
5. Tétel: Legyen ${\sc P}$ egy $({\sc T},2,1,B)$ kép, és legyen $p ∈ B$. A $p$ pixel akkor és csak akkor egyszerű, ha a csatolt halmaza és annak komplementere egyszerre nemüres és összefüggő.
Példa: A 9. ábrán négy $\sc T$ mozaikbeli pixel szomszédsági konfigurációja és csatolt halmazai láthatók. A csatolt halmazhoz tartozó élek és csúcsok piros színnel, a csatolt halmaz komplementérehez tartozó élek és csúcsok zöld színnel vannak jelölve. Vegyük észre, hogy csak az a)konfiguráció reprezentál egyszerű pixelt.
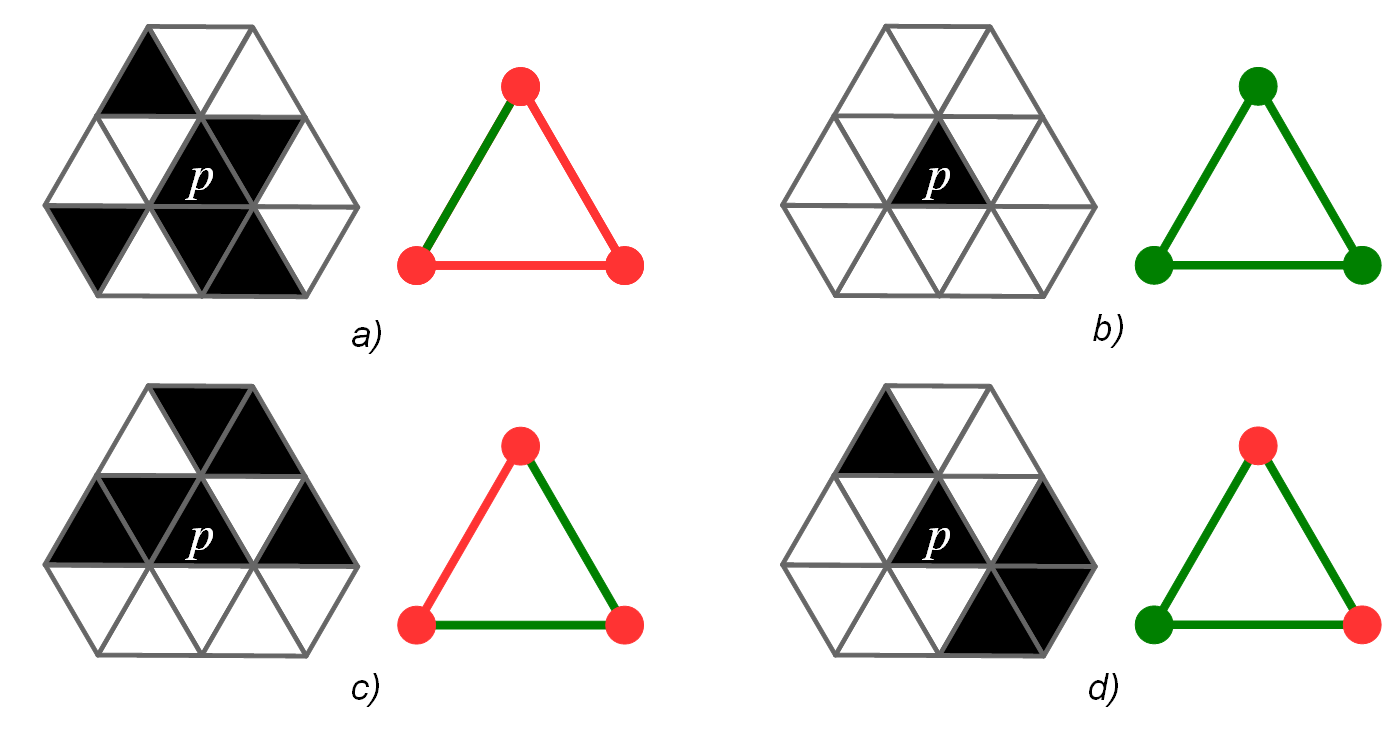
15. ábra. Példák egyszerű és nem egyszerű pixelek konfigurációira és csatolt halmazaira
Elegendő feltételek topológia-megőrző redukciókra
A háromszög-mozaikon mintavételezett képek topológia-megőrző redukcióira először [7]-ben javasoltunk elegendő feltételeket.6. Tétel: [7] Az ${\sc R}$ redukció topológia-megőrző, ha valamennyi $(\sc T, k, \ov{k}, B)$ képre $((k,\ov {k}) = (2,1), (1,2))$ teljesülnek az alábbi feltételek:
- Valamennyi ${\sc R}$ által törölt pixel egyszerű.
- Valamennyi ${\sc R}$ által törölt, egymással $k$-szomszédos pixelpár (lásd a 16. ábrát) egyszerű halmazt alkot.
- ${\sc R}$ nem töröl teljesen egyetlen olyan kis objektumot sem, amelynek bármely két pixele 2-szomszédos egymással (lásd a 17. ábrát).
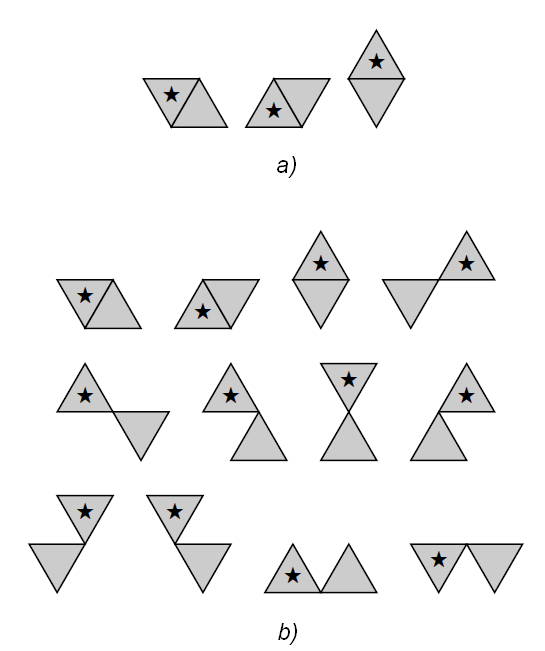
16. ábra. Lehetséges pixelpárosok a $\sc T$ mozaikon mintvételezett (2,1) (a) és (1,2) (b) képeken. Egy-egy pár kitüntetett elemét '∗' jelöli.

17. ábra. A lehetséges kis objektumok a $\sc T$ mozaikon mintvételezett (2,1)képeken. Egy-egy kis objektum kitüntetett elemét '∗' jelöli.
7. Tétel: Az ${\sc R}$ redukció topológia-megőrző a $\sc P =(\sc T, k, \ov{k}, B)$ képre, ha a kép valamennyi ${\sc R}$ által törölt $p$ pixelére teljesülnek az alábbiak:
- $p$ egyszerű a $\sc P$ képen.
- Bármely egyszerű $q ∈ N^{*}_2(p)$ pixelre, $p$ egyszerű a $(\sc T, k, \ov{k}, B ∖ \{q \})$ képen.
- $(k,\ov{k}) = (2,1)$ esetben $p$ nem eleme egyetlen kis objektumnak sem (lásd 17. ábra).
8. Tétel: Az ${\sc R}$ redukció topológia-megőrző a $\sc P =(\sc T, k, \ov{k}, B)$ képre, ha a kép valamennyi ${\sc R}$ által törölt $p$ pixelére teljesülnek az alábbiak:
- $p$ egyszerű a $\sc P$ képen.
- Bármely egyszerű $q ∈ N^{*}_2(p)$ pixelre, $p$ egyszerű a $(\sc T, k, \ov{k}, B ∖ \{q \})$ képen, vagy $q$ a $\{p,q \}$ pár kitüntetett eleme (lásd a 16. ábrát).
- $(k,\ov{k}) = (2,1)$ esetben $p$ nem kitüntetett eleme egyetlen kis objektumnak sem (lásd a 17. ábrát).
