Vázkijelölés vékonyítással
A váz fogalma
A vázkijelölés során az objektumok minden egyes pontjához megkeressük a hozzá legközelebb eső határponto(ka)t. [6] Ha valamely belső ponthoz egynél több legközelebbi határpontot találunk, akkor az illető pont a vázhoz tartozik. A váz szemléletesen definiálható a préritűz-hasonlattal : ha az objektum határának minden pontjában egyszerre tüzet gyújtunk, és a tűzfrontok minden irányban egyenletes sebességgel terjednek, akkor a váz azon pontok mértani helye, ahol a tűzfrontok találkoznak és kioltják egymást.
Diszkrét esetben a (folytonos) váz helyett az ún. vázszerű jellemzők meghatározása a cél. A 2D objektumok két vázszerű alakjellemzője a középvonal és a topológiai mag. A középvonal a folytonos váz közelítésére szolgál, míg egy topológiai mag topológia-megőrző redukcióval áll elő a kiindulási objektumból és nem tartalmaz egyszerű pontot.
A vékonyítás (mint a leggyakrabban alkalmazott vázkijelölő módszer) iteratív objektum-redukció, melynek egy lépésében az aktuális objektum határpontjai közül a törölhetőnek minősítetteket távolítjuk el. Az eljárás terminál, ha az objektumon már nincs több törölhető pont. Az eredményül kapott kép a bemeneti kép objektumainak vázszerű jellemzőit tartalmazza (lásd 11. ábra).
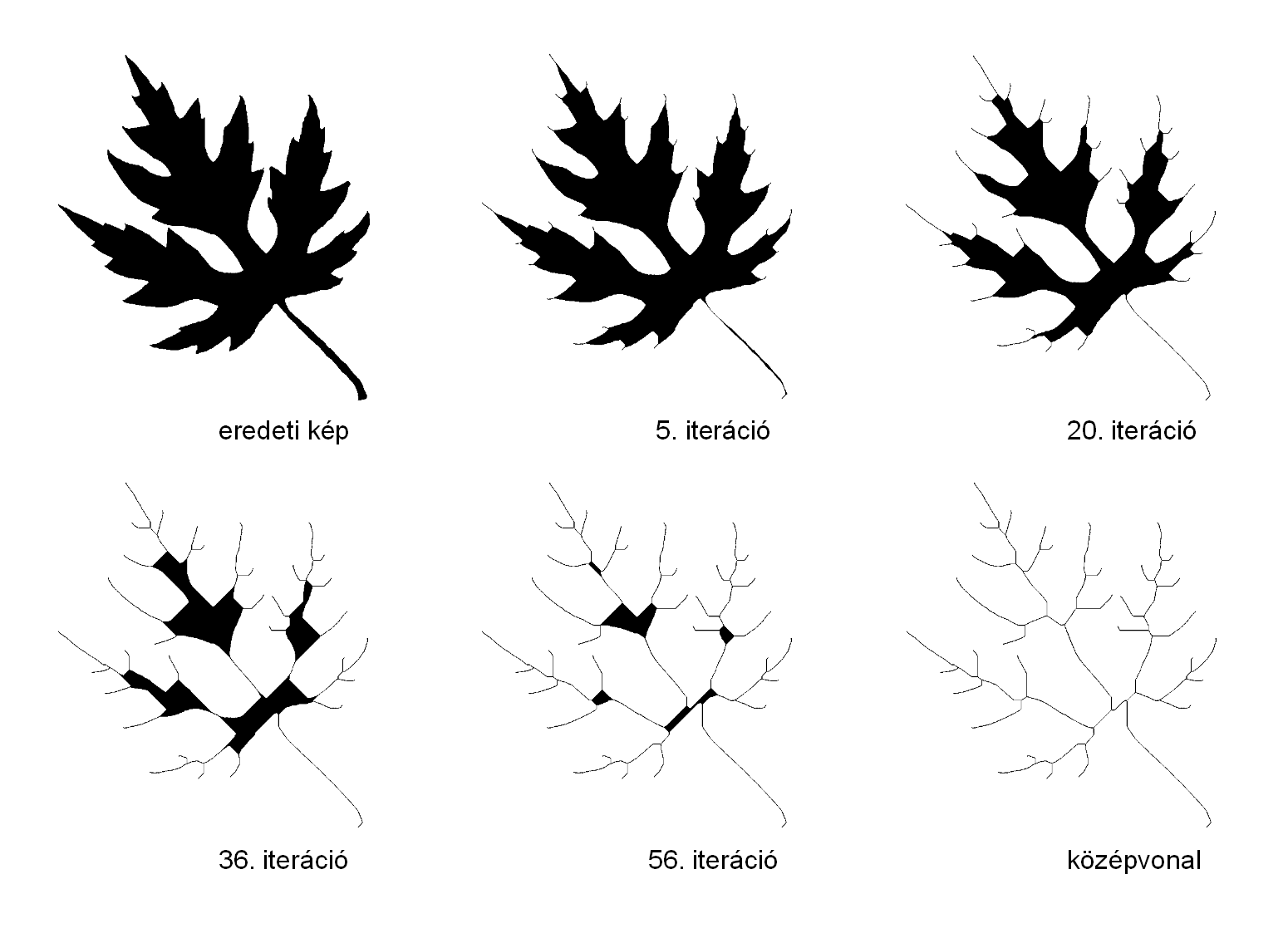
11. ábra. Példa vékonyításra.
Párhuzamos vékonyító stratégiák
Attól függően, hogy egyszerre egy vagy több határpont törléséről döntünk, megkülönböztethetünk szekvenciális és párhuzamos vékonyító technikákat. [4] Jelen kutatási témában csak párhuzamos algoritmusokkal foglalkozunk, melyeknek három fő változatát különböztethetjük meg: a teljesen párhuzamos, az irány-alapú, ill. az almező alapú eljárásokat.
Teljesen párhuzamos vékonyítás
A teljesen párhuzamos stratégiát követő algoritmusok egy iterációs lépése során mindössze egyetlen redukció hajtódik végre, melynek során valamennyi törölhetőnek minősülő képelem egyidejűleg törlődik (lásd 12. ábra).
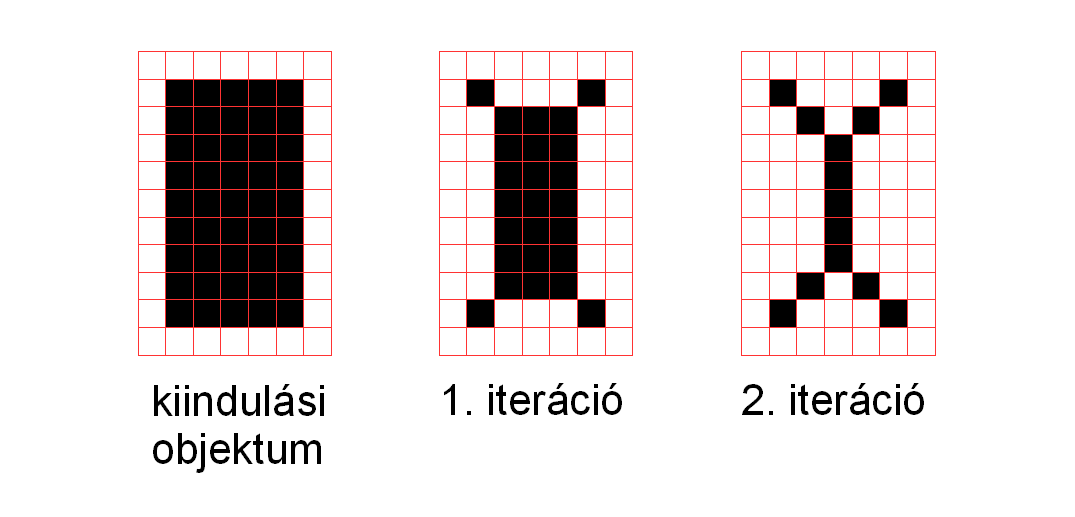
12. ábra.
Irány-alapú vékonyítás
Az irány-alapú eljárások egyes aliterációiban csak adott irányú határpontokat ellenőrzünk. Egy iterációs lépés során egymást követően legalább két redukciót alkalmazunk, melyek szekvenciáját az algoritmusra jellemző törlési irány-sorozat határozza meg. A 13. ábra a négy fő irány (észak, kelet, dél, nyugat)szerinti vékonyítást mutatja be.
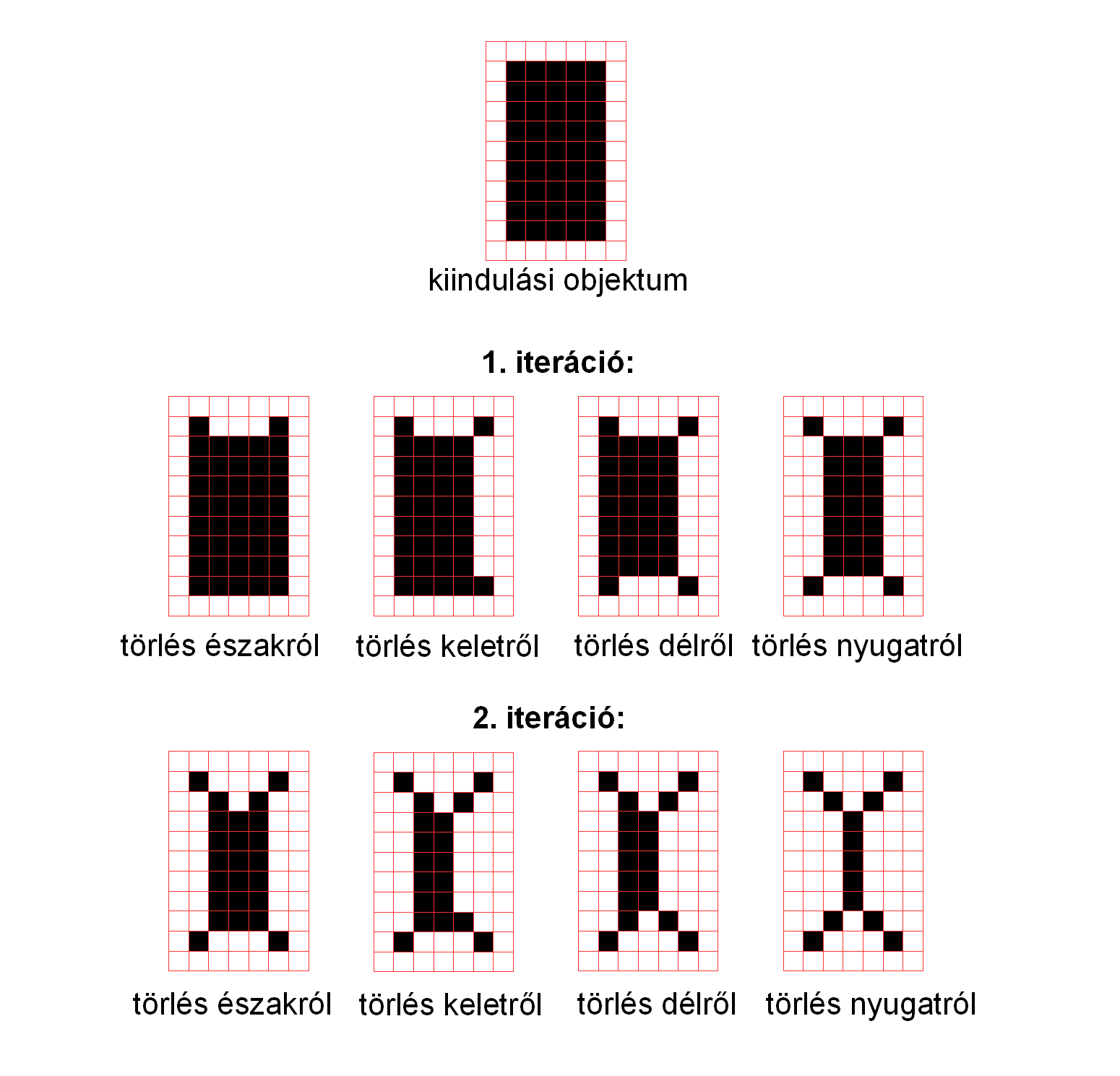
13. ábra
Almező-alapú vékonyítás
Az almező-alapú stratégia a képelemek halmazának diszjunkt részhalmazokra, ún. almezőkre történő particionálásán alapul. Az ezen elven működő algoritmusok egy iterációs lépése során az almezőket egymás után aktiváljuk, és az adott aliterációban csak az aktív almezőbe eső pontokat vizsgáljuk. A 14. ábra egy két almezőt megkülönböztető vékonyító algoritmus működését illusztrálja.
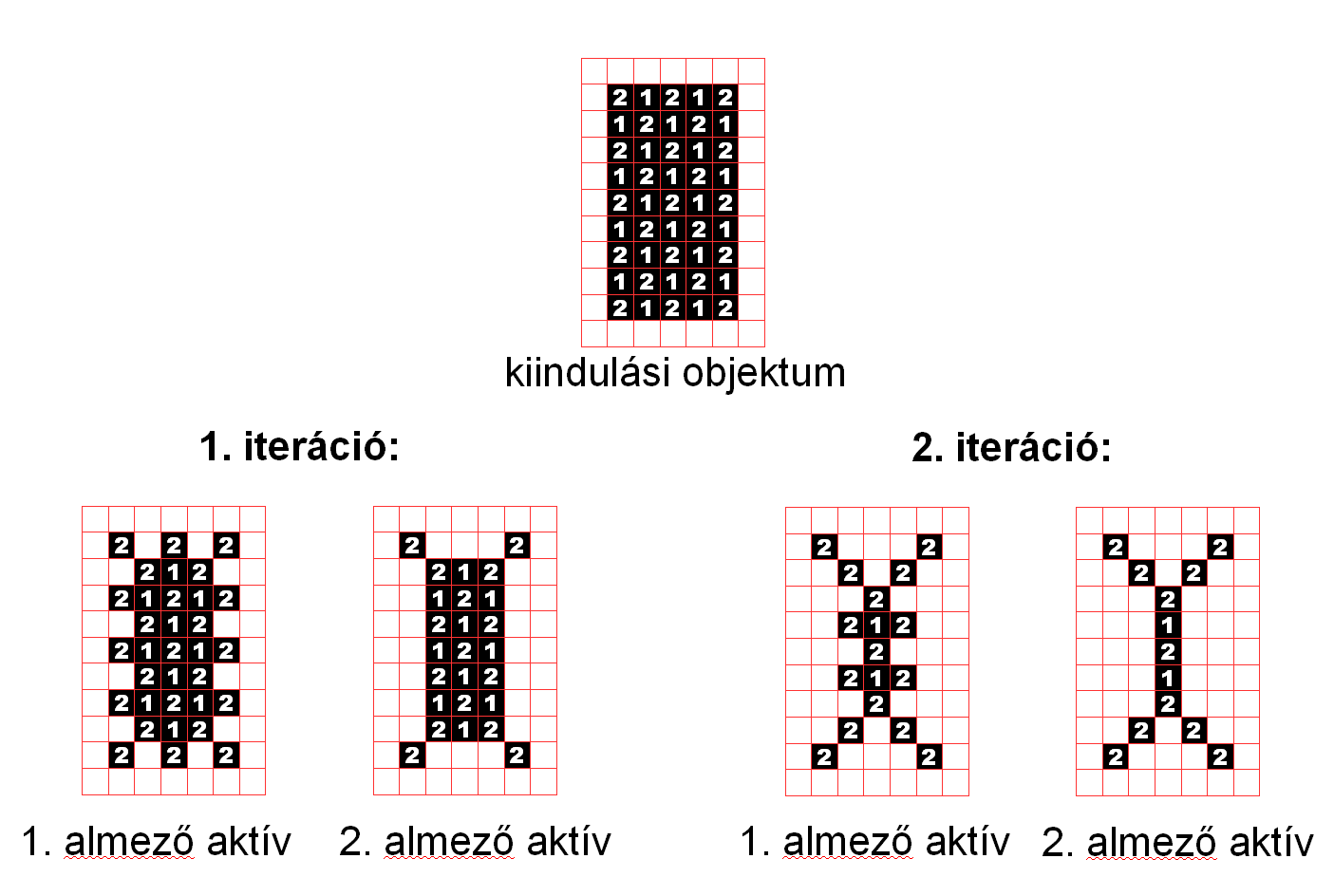
14. ábra
