Digitális topológia
A digitális topológia a bináris digitális képek topológiai tulajdonságaival foglalkozik. A legfontosabb kérdése az, hogy az egyes képműveletek megőrzik-e a topológiát. Az alábbiakban Kong és Rosenfeld áttekintő munkájának [2] jelöléseit és tárgyalásmódját követem.
2D mozaikok és rácsok
A 2D euklideszi síkon uniform mintavételezésekkel szabályos poligonokra particionáljuk. [4] 2D-ben csak három szabályos mozaik létezik, vagyis csak a szabályos háromszög, a négyzet, a szabályos hatszög, ill. a kocka egybevágó példányaival lehetséges átfedések nélkül és hézagmentesen lefedni a teret(lásd 1-3. ábrák. A szabályos mozaikok poligonjai egy-egy képlemet határoznak meg, amelyeket pixeleknek nevezzük. Valamennyi szabályos mozaikhoz megadható egy-egy duális rács, amelyek rácspontjainak halmazát a kiinduló mozaik poligonjainak középpontjai alkotják, az élek az élen osztozó poligonok középpontjait kötik össze.
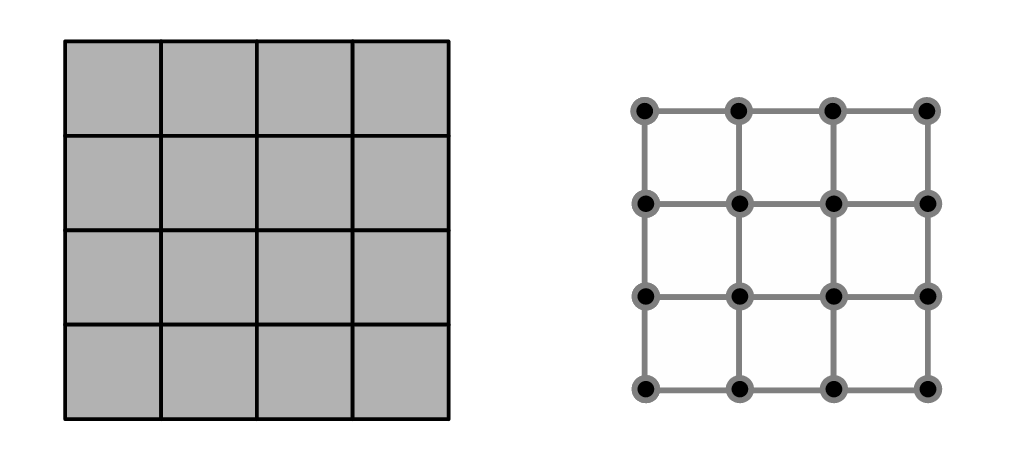
1. ábra
Négyzet-mozaik és négyzet-rács
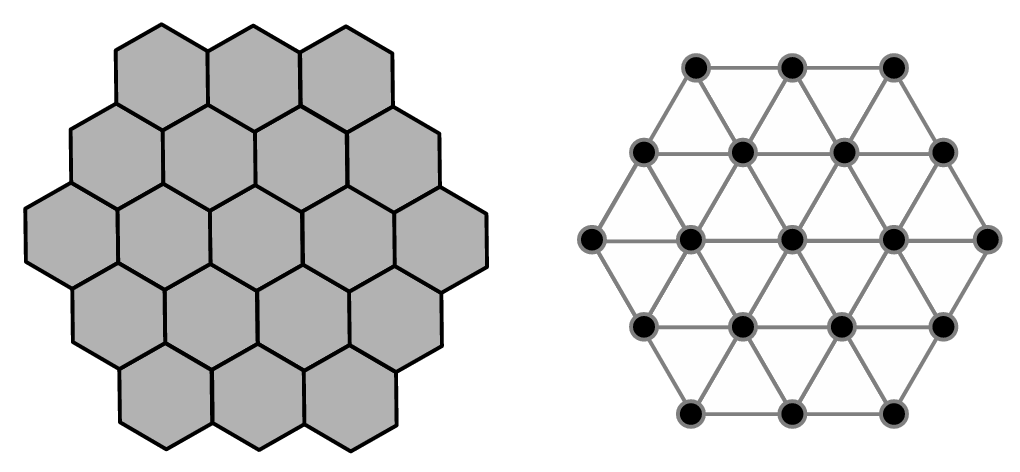
2. ábra
Hatszögmozaik és hatszögrács
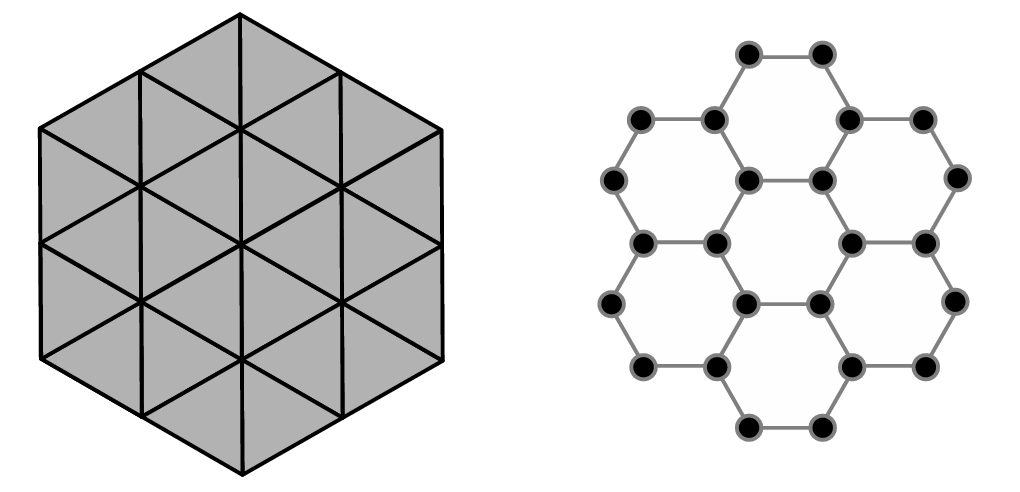
3. ábra
Háromszög-mozaik és háromszög-rács
Szomszédsági relációk
A figyelembevett 2D mozaikokon mintavételezett képeken két poligon (pixel) 1-szomszédos ill. 2-szomszédos, ha azok rendre élen ill. élen vagy csúcson érintkeznek (lásd 4. ábra).
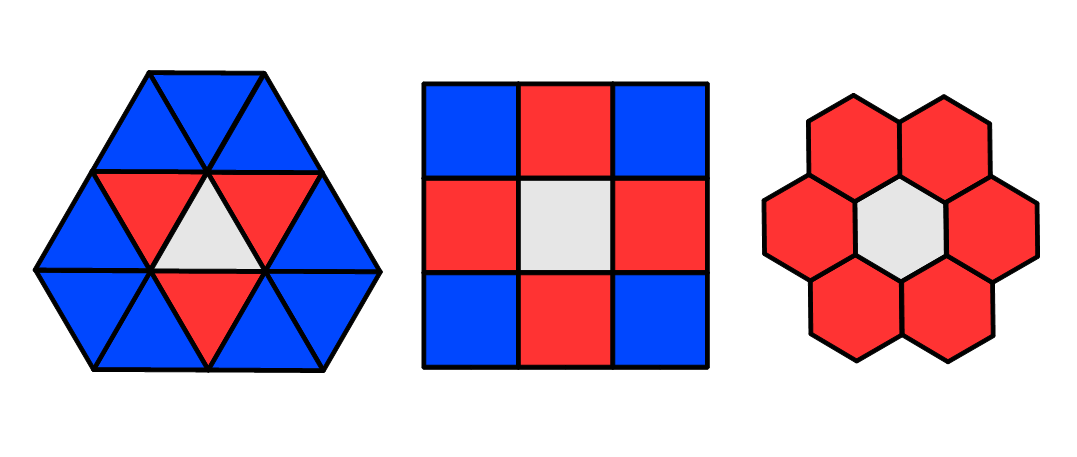
4. ábra
Szomszédsági típusok a 2D mozaikokon: a piros elemek a középsőnek 1-szomszédai, a kék elemek pedig a középsőnek 2-szomszédai, de nem 1-szomszédai.
Egység-elem
Az $V$ mozaik azon pontjainak maximális halmazát, melynek bármely két eleme 2-szomszédos, a $V$ egység-elemének nevezzük (lásd 5. ábra).

5. ábra. Egység-elemek a háromszög-, négyszög-, és hatszög-mozaikon
Összefüggőség, komponensek
Pixeleknek egy S halmaza m-összefüggő (m=1,2), ha S bármely két p,q eleméhez megadható olyan pixel-sorozat, amelyre:
- p a sorozat első eleme,
- q a sorozat utolsó eleme, és
- a sorozat bármely két egymást követő eleme k-szomszédos.
Példa: az 5. ábra az 1- és 2- összefüggőség közötti különbséget illusztrálja.
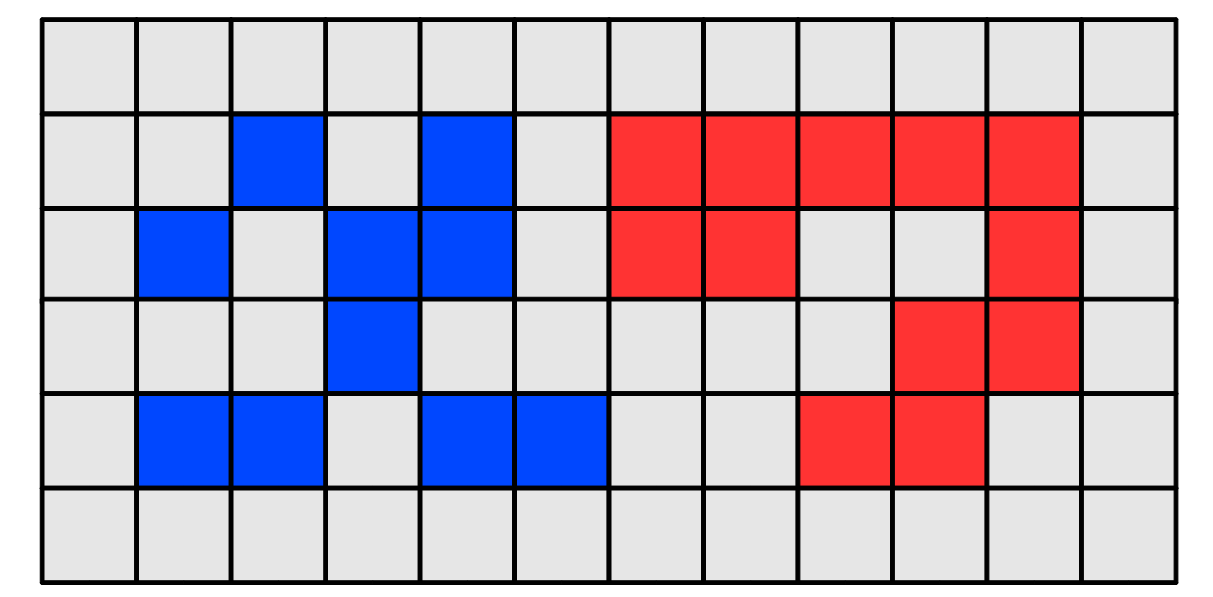
6. ábra
A kék pixelek halmaza 2-, de nem 1-összefüggő, míg a piros pixelek halmaza 2- és 1-összefüggő is.
Bináris digitális kép
A bináris képek elemei mindössze kettő, a 0 és az 1 értékeket vehetik fel. A digitális bináris képet olyan rendezett ${\sc{P}}=(V,k,\ov{k},B)$ négyessel írjuk le, ahol:
- V a képlemek halmaza,
- A $B ⊆ V$ halmaz a fekete képlemek halmaza, melynek $\ov B$ komplementere a fehér képelemek halmaza.
- $k$-összefüggőséget tételezünk fel a $B$ halmazra, vagyis a fekete képelemekre,
- $\ov k$-összefüggőséget veszünk figyelembe a fehér képelemekre.
Objektum, üreg
A $\sc P$ digitális kép véges, ha $B$ véges. Digitális bináris képeken a fekete $k$-komponenseket objektumoknak nevezzük. A véges képeken levő egyetlen végtelen fehér $\ov k$-komponenst háttérnek nevezzük, a véges fehér $\ov k$-komponensek pedig a kép üregei. Egy fekete pont izolált, ha egymaga alkot objektumot.

7. ábra. Háromszögmozaikon mintavételezett bináris digitális kép
Határpont, belső pont
A $p ∈ B$ képelem határpont a $(V,k,\ov{k},B)$ képen, ha $p$ $\ov{k}$-szomszédos legalább egy fehér ponttal. Ha egy $p ∈ B$ pont nem határpont, akkor azt belső pontnak nevezzük.
Topológia-megőrző redukciók
A $V$ képpont-halmazon az $\sc{O}$ képművelet egy $P(V)→ P(V)$ leképezés, ahol $P(V)$ a $V$ halmaz hatványhalmazát jelöli. Az $\sc O$ képművelet eredményeként a $(V,k,\ov k,B)$ képből a $(V,k,\ov k,{\sc{O}}(B))$ képet kapjuk. Ha $\sc O(B)⊆ B$ valamennyi $B ⊆ V$ halmazra teljesül, akkor az $\sc O$ képművelet redukció.
Egy 2D redukció topológia-megőrző, ha az alábbi feltételeket teljesíti:
- nem szakít szét (kettő vagy több darabra) objektumot.
- nem töröl teljesen objektumot.
- nem olvaszt össze üreget sem másik üreggel, sem pedig a háttérrel.
- nem hoz létre új üreget.
Példa: a 8. ábra egy olyan redukciót mutat be, amely a fenti kritériumok egyikét sem elégíti ki, azaz nem őrzi meg a topológiát.
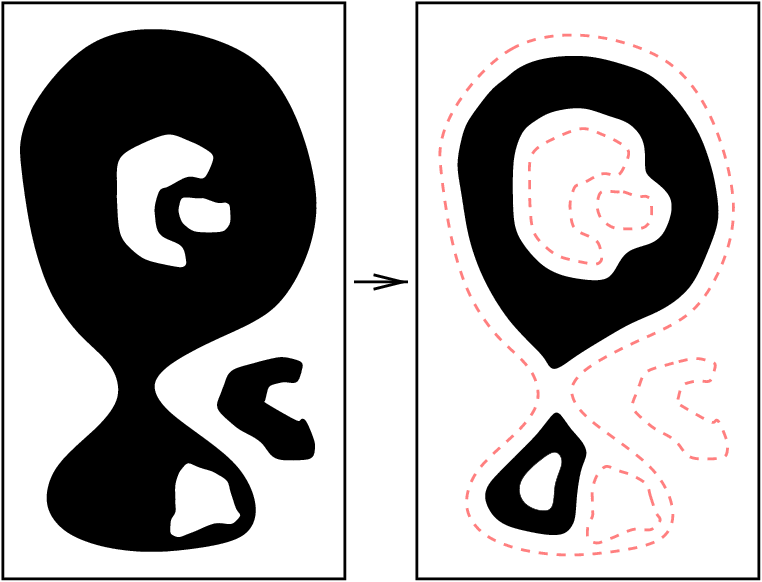
8. ábra. Példa egy nem topológia-megőrző redukcióra
Egyszerű pixelek
A $p$ fekete pixel egyszerű egy $(V,k,\ov{k},B)$ képen, ha törlése egy topológia-megőrző művelet (azaz a kép topológiája nem függ $p$ színétől.
Az egyszerű képelemek jellemzésére ill. a topológia korrektség vizsgálatára korábban csak négyzet- és kocka-mozaikon mintavételezett képeken értelmezett redukciókra adtak kritériumokat.
1. Tétel: Legyen $p ∈ B$ a $({\sc S},k,\ov{k},B)$ $((k,\ov{k})=(2,1),(1,2))$ képnek egy nem-izolált határpixele.
- $p$ egyszerű pixel.
- $p$ pontosan egy $N^{*}_2(p)∩ B$ halmazbeli $k$-komponenssel $k$-szomszédos.
- $p$ pontosan egy $N^_2(p)∖ B$ halmazbeli $\ov{k}$-komponenssel $\ov{k}$-szomszédos.
Kong az egyszerűség vizsgálatára egy további módszert javasolt, amely az ún. "csatolt halmazok" fogalmán alapszik [1]. Ez a modell a pixelhez a 3x3-as környezete alapján hozzárendeli egy négyzet csúcsainak és éleinek egy részhalmazát, melyet a pixel csatolt halmazának nevezünk. Ily módon tehát a pixelek egyszerűsége(mint diszkrét képeken eldöntendő tulajdonságot)folytonos halmazok összefüggőségére vezethető vissza. A csatolt halmaz képzése az alábbi szabályok szerint történik:
- Ha a $p$ pontnak az $(S,2,1,B)$ képen a felső 1-szomszédja fekete, akkor a csatolt halmaz tartalmazza a felső élet a végpontjaival együtt.
- Ha a $p$ pontnak az $(S,2,1,B)$ képen a bal-felső 2-szomszédja fekete, akkor a csatolt halmaz tartalazza a bal-felső csúcsot.
- A többi irányban elhelyezkedő 1- és 2-szomszéd esetén a fentiekhez hasonló módon állapítható meg az, hogy mely éleket ill. csúcsokat tartalmazza a csatolt halmaz.
2. Tétel: Az (S,2,1,B) képen a $p$ pixel akkor és csak akkor egyszerű, ha $p$ csatolt halmaza és annak komplementere egyszerre összefüggő és nem üres. (Csatolt halmaz komplementerénél a négyzet négy éléből és négy csúcsából álló halmazt (mint univerzumot)kell figyelembe venni.)
Példa: A 9. ábrán négy $\sc S$ mozaikbeli pixel szomszédsági konfigurációja, mellettük pedig a nekik megfelelő csatolt halmazok láthatók. A csatolt halmazhoz tartozó élek és csúcsok piros színnel, a csatolt halmaz komplementérehez tartozó élek és csúcsok zöld színnel vannak jelölve. Vegyük észre, hogy csak az a)konfiguráció reprezentál egyszerű pixelt.
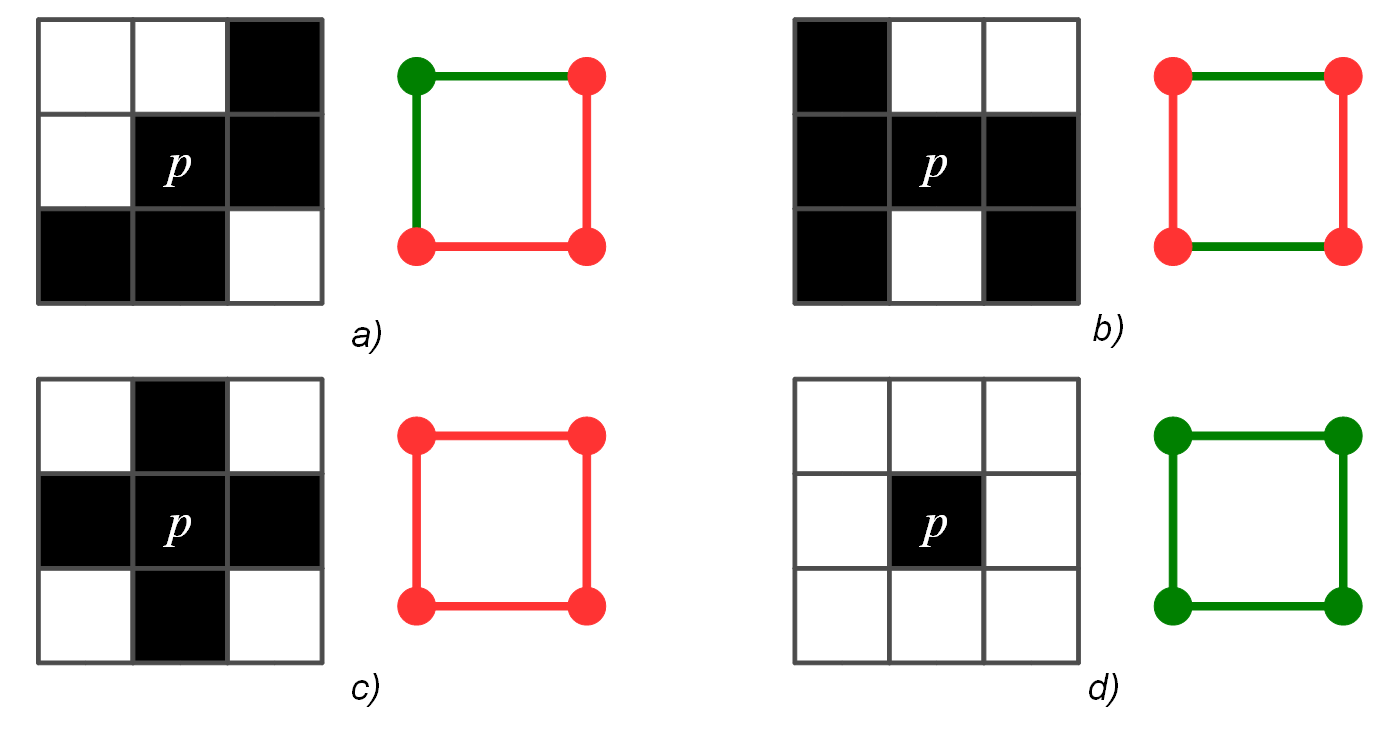
9. ábra. Példák csatolt halmazokra az $\sc S$ mozaikon
Topológia-megőrzés elegendő feltételei
Egyetlen egyszerű képelem törlése - definíció szerint - topológia-megőrző redukció, azonban több elemet tartalmazó képelem-halmazok törlésénél a topológiai korrektség nem mindig áll fenn.
Példa: legyen $\sc P = (S,2,1,B)$ a 10. ábrán levő kép, és legyen $\sc R$ az a redukció, amely $\sc P$-ről a $*$-gal jelölt fekete pixeleket törli. Könnyen ellenőrizhető, hogy a törölt pixelek mindegyike egyszerű, azonban $\sc R$ nem topológia-megőrző, hiszen egy objektumot három komponensre szakít, valamint egy objektumot teljesen töröl.

10. ábra. Példa olyan topológia-megőrző redukcióra, amely csak egyszerű pontokat töröl
2D redukciók topológia-megőrzésére Ronse dolgozta ki az alábbi elegendő feltételeket.
3. Tétel : [5] AZ $\sc{R}$ redukció topológia-megőrző, ha valamennyi $({\sc S}, k,\ov k,B)$ képre $((k,\ov{k})=(2,1),(1,2))$ teljesülnek az alábbi feltételek.
- Valamennyi $\sc{R}$ által törölt pixel egyszerű.
- Valamennyi $\sc{R}$ által törölt, egymással $\ov k$-szomszédos pixelpár egyszerű halmazt alkot.
- Ha $(k,\ov {k})=(2,1)$, akkor $\sc{R}$ nem töröl teljesen egyetlen egység-elembe foglalható objektumot sem.
