Trianguláris vékonyítás

Topológia-megőrző trianguláris vékonyító algoritmusok

Az előzőekben bemutatott párhuzamos vékonyító stratégiákkal és változatos geometriai kényszerfeltételekkel kombinálva olyan új trianguláris (azaz a háromszögmozaikon mintavételezett képekre érvényes) eljárásokat konstruáltunk, amelyek topológia-megőrző volta bonyolult és terjengős bizonyítások nélkül is garantált a
6-8. Tételek alapján.

A javasolt algoritmusok elnevezésekor a következőképpen jártam el: az ${\sc T}$-$FP$-$ß$-$ε$ algoritmusok a teljesen párhuzamos stratégiát követik, az ${\sc T}$-$SI$-$ß$-$ε$ eljárások irány alapúak (egységesen 6 aliterációval), és az ${\sc T}$-$SF_l$-$ß$-$ε$ algoritmusok pedig $l$ almezővel dolgozó almező-alapúak, ahol:

$ß$: arra utal, hogy az adott algoritmus szimmetrikus vagy aszimmetrikus elegendő feltételeken alapul-e. Lehetséges értékei: SYM (szimmetrikus), ASYM (aszimmetrikus.
$ε$: a figyelembevett végpixelek (mint geometriai kényszerfeltételek) lehetséges típusai. Itt az $E_0$ ill.\ $E_1$ típusokat különböztettem meg, melyek az alábbi jelentéssel bírnak:
- $ε=E_0$ esetben nem teszünk korlátozást, geometriai kényszerfeltételt. Bevezetését az indokolja, hogy a zsugorító és a további típusú végpontpixeleket megőrző, középvonalra vékonyító algoritmusokat egységesen kezelhessem.
- $ε=E_1$ esetben végpixelnek tekintem az olyan egyszerű fekete pixelt, amelynek legfeljebb kettő valódi fekete 2-szomszédja és legfeljebb 1 valódi fekete 1-szomszédja van.

Teljesen párhuzamos algoritmusok

A teljesen párhuzamos vékonyító algoritmusaink sémáját az alábbi algoritmus vázolja fel:


Algoritmus: $\sc T$-$FP$-$ß$-$ε$
Input: az $({\sc T},2,1,X)$ kép 
Output: az $({\sc T},2,1,Y)$ kép
$Y=X$
repeat
  $D=\{p|p$ ${\sc T}$-$FP$-$ß$-$ε$-törölhető az $Y$ képen $\}$;
  $Y= Y \\ D$;
until $D=Ř$

A könnyebb érthetőség végett algoritmusaink működését egy egyszerű objektumra mutatjuk be a 18. ábrán.

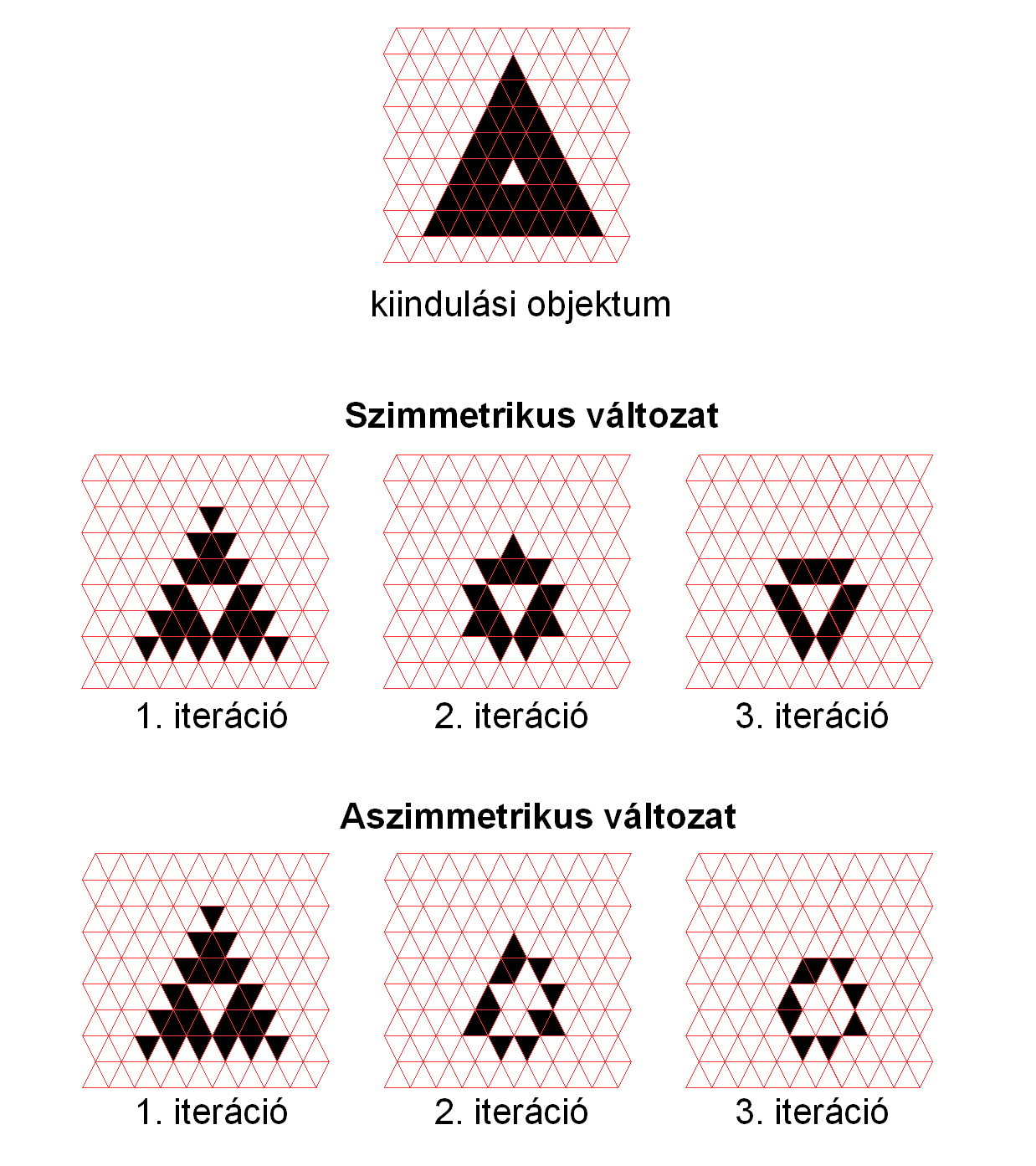
18. ábra

Az ${\sc T}$-$FP$-$ß$-$ε$-törölhető pixeleket a következőképpen definiáljuk.

Definíció: A $p$ fekete pixel ${\sc T}$-$FP$-$ß$-SYMM-$ε$-törölhető, ha nem $ε$-végpixel és kielégíti az 5. tétel feltételeit.
Definíció: A $p$ fekete pixel ${\sc T}$-$FP$-$ß$-$ε$-ASYM-törölhető, ha nem $ε$-végpixel és kielégíti a 6. tétel feltételeit.

Irány-alapú párhuzamos algoritmusok

A $\sc T$ mozaikon mintavételezett képekre olyan irány-alapú algoritmusokat konstruáltunk, amelyeknél egy iterációs lépés 6 al-iterációból áll. Az egyes al-iterációk redukcióiban csak az adott típusú határpixelek törlődhetnek. A törölhető pixelek meghatározásához bevezetünk egy további fogalmat: a $({\sc T}, 2,1, B)$ képeken $d$-határpixelnek nevezzük azon határpixeleket, amelyeknek a 19. ábra jelölése szerinti $p_d$ 1-szomszédjuk fehér $(d=1,...,6)$.

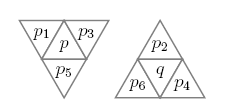
19. ábra. A határpixelek megkülönböztetése hat irány szerint

Az hat-irányú algoritmus működését a 20. ábra szemlélteti.


Algoritmus: ${\sc T}$-$SI$-$ε$
Input: az $({\sc T},2,1,X)$ kép 
Output: az $({\sc T},2,1,Y)$ kép
$Y=X$
$I=Ř$
repeat
  $D=Ř$
  for $d$=1 to 6 do
  $D_d=\{p|p$ ${\sc T}$-$SI$-$d$-$?$-törölhető az $Y$ képen $\}$;
  $Y= Y$ \ $D$;
  $D= D$ ? $D_d$;
until $D=Ř$

Az ${\sc T}$-SI-$ß$-$ε$ algoritmusok egyes aliterációiban a törölhető pixeleket az alábbi négy definícióval adjuk meg:

Definíció: A $p$ fekete pixel $\sc T$-SI-$d$-$ε$-törölhető $(? ? \{E_0,E^{\sc T}_1\}, d=1, ..., 6 )$, ha az alábbi feltételek mindegyike teljesül:

$p$ egyszerű, de nem $ε$-végpixel és $d$-határpixel.
Ha $? = E_0$, akkor $p$ nem kitüntetett eleme kettő vagy három $d$-határpixelből álló kis objektumnak.

20. ábra

Almező-alapú párhuzamos algoritmusok

A $\sc T$ mozaikot a 21. ábrán látható kétféle mintázat szerint osztjuk fel 2 ill. 4 almezőre.

21. ábra. Felbontás 2 (bal) ill. 4 (jobb) almezőre

Almező-alapú eljárásaink alábbi pszeudo-kódjában az $l$ paraméter utal a használt almezős felbontás típusára.


Algoritmus: ${\sc T}$-$SF_l$-$ε$
Input: az $({\sc T},2,1,X)$ kép 
Output: az $({\sc T},2,1,Y)$ kép
$Y=X$
$I=Ř$
repeat
  $D=Ř$
  $E=\{p|p$ határpixel de nem $?$-végpixel az $Y$ képen$\}$
  for $i$=0 to $l-1$ do
  $D_i=\{p|p$ ${\sc T}$-$SF$-$l$-$i$-$ß$-$?$-törölhető az $Y$ képen $\}$;
  $Y= Y$ \ $D_i$;
  $D= D$ ? $D_i$;
until $D=Ř$

Az algoritmus által vizsgált ${\sc T}$-SF-$l$-$i$-$ε$-törölhető pixeleket az alábbi módon értelmezzük.

Definíció: A $p$ fekete pixel $\sc T$-SF-$l$-$i$-$ε$-törölhető, ha az alábbiak teljesülnek:

$p ? SF^{\sc T}_{l}(i)$ $(l=2,4; i=0, ..., l-1)$ és $p$ egyszerű pixel.
Ha $? = E_0$, akkor $p$ nem kitüntetett eleme egyetlen olyan $\{p,q \}$ vagy $\{p,q,r\}$ kis objektumnak sem, amelyekre $q,r ? SF^{\sc T}_{l}(i)$.

A két-almezős algoritmust a 22. ábra illusztrálja.

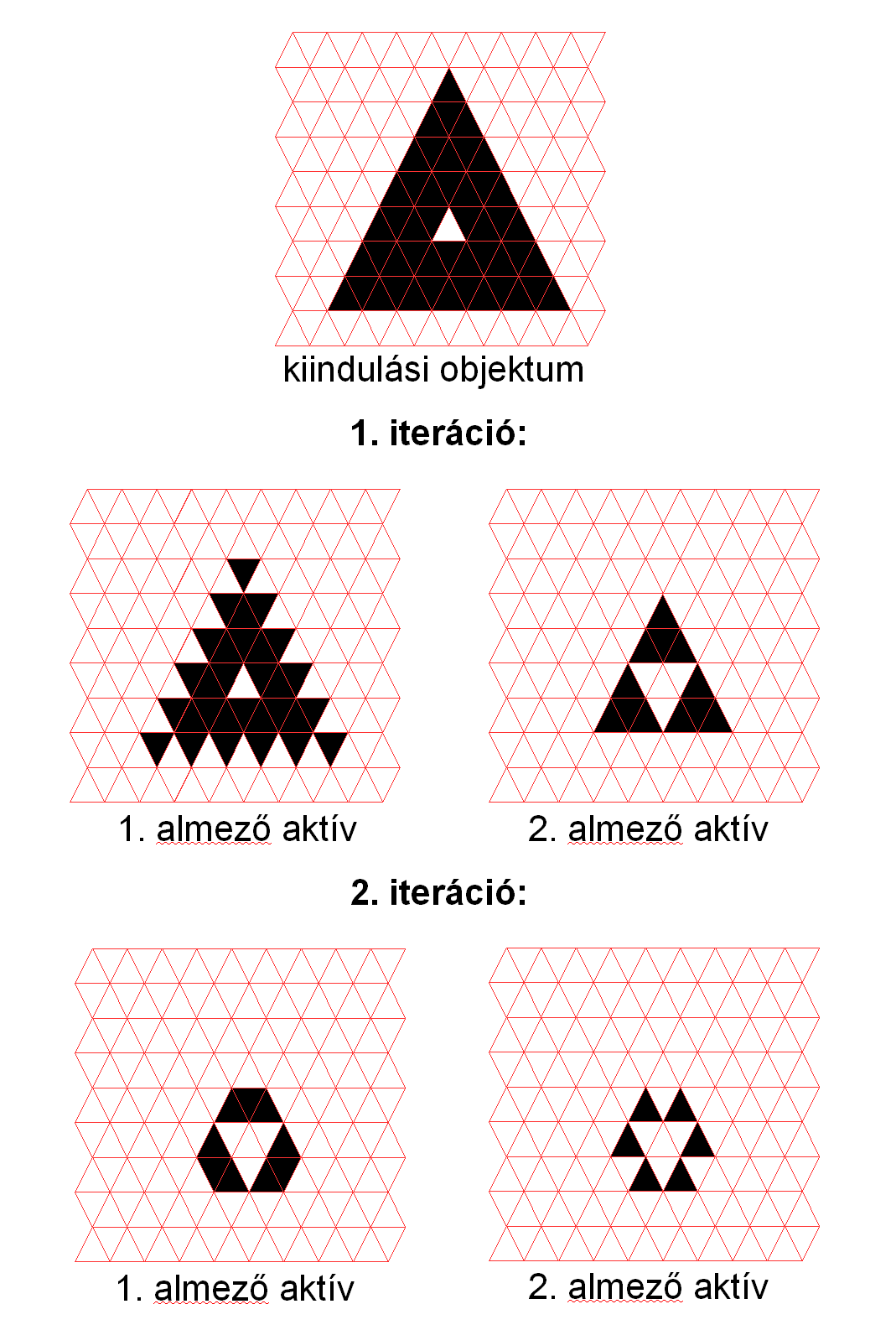
22. ábra