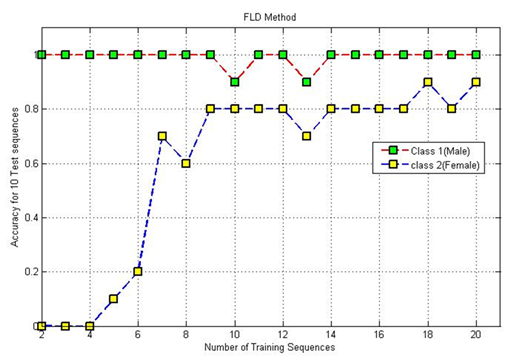
Linear discriminate analysis (LDA) and the related Fisher's linear discriminate are methods used in statistics and machine learning to find the linear combination of features which best separate two or more classes of objects or events. The resulting combination may be used as a linear classifier, or, more commonly, for dimensionality reduction before later classification.

LDA is closely related to ANOVA (analysis of variance) and regression analysis, which also attempt to express one dependent variable as a linear combination of other features or measurements. In the other two methods however, the dependent variable is a numerical quantity, while for LDA it is a categorical variable (i.e. the class label).

LDA is also closely related to principal component analysis (PCA) and factor analysis in that both look for linear combinations of variables which best explain the data. LDA explicitly attempts to model the difference between the classes of data. PCA on the other hand does not take into account any difference in class, and factor analysis builds the feature combinations based on differences rather than similarities. Discriminate analysis is also different from factor analysis in that it is not an interdependence technique : a distinction between independent variables and dependent variables (also called criterion variables) must be made.

LDA works when the measurements made on each observation are continuous quantities. When dealing with categorical variables, the equivalent technique is Discriminate.

Þ PCA

Þ FLD

Þ CV

Þ SVM

Þ PCA + SVM

SSIP 2008 16th summer school on Image processing July 7th -16th 2008 Vienna