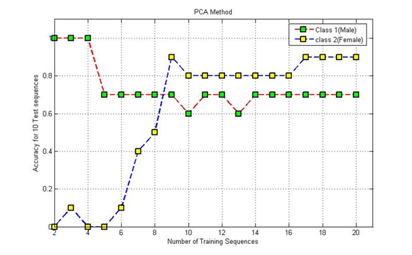
Principal component analysis (PCA) is a vector space transform often used to reduce multidimensional data sets to lower dimensions for analysis. Depending on the field of application, it is also named the discrete Karhunen-Loève transform, the Hotelling transform or proper orthogonal decomposition (POD).

PCA involves the calculation of the Eigenvalue decomposition of a data covariance matrix or singular value decomposition of a data matrix, usually after mean centering the data for each attribute. The results of a PCA are usually discussed in terms of component scores and loadings (Shaw, 2003).

PCA is the simplest and most useful of the true eigenvector-based multivariate analyses, because its operation is to reveal the internal structure of data in an unbiased way. If a multivariate dataset is visualized as a set of coordinates in a high-dimensional data space (1 axis per variable), PCA supplies the user with a 2D picture, a shadow of this object when viewed from its most informative viewpoint. This dimensionally-reduced image of the data is the ordination diagram of the 1st two principal axes of the data, which when combined with metadata (such as gender, location etc) can rapidly reveal the main factors underlying the structure of data. PCA is especially useful for taming collinear data; where multiple variables are co-correlated (which is routine in multivariate data) regression-based techniques are unreliable and can give misleading outputs, whereas PCA will combine all collinear data into a small number of independent (orthogonal) axes, which can then safely be used for further analyses.

Þ PCA

Þ FLD

Þ CV

Þ SVM

Þ PCA & SVM

SSIP 2008 16th summer school on Image processing July 7th -16th 2008 Vienna