Saját felszínháló létrehozása

Háromszögháló

3D objektumok felszínét háromszögekkel közelíthetjük. A háromszögek térbeli csúcspont koordinátáit ugyanúgy a geometria vertices listájában adjuk meg, mint a pontfelhő és a vonalak esetén. Emellett meg kell adni egy lap listát (faces), amely a vertices lista elemeinek indexeiből épül fel. Három index definiál egy háromszöget, amit Face3 objektumpéldányokként kell előállítani és a lap listához adni.

Anyagként a korábban, a Three.js beépített objektumainál megismertek használhatók (pl. MeshBasicMaterial, MeshLambertMaterial, MeshPhongMaterial). Az utóbbi kettő csak akkor működik, ha normálvektorokat is megadunk a lapokhoz, ami a fény beesési szögének számításához elengedhetetlen.

Felszínháló felépítése

Trapéz modellezése példa

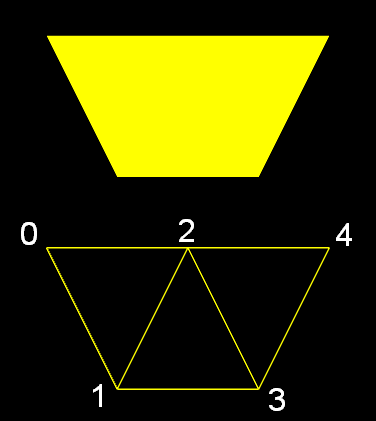Példaként egy trapéz modellt készítünk, amit 3 darab háromszögből építünk fel.

Induljunk ki a ThreeJsTrapeziumSkeleton vázból, ami interaktív kameramozgatást tesz lehetővé, beállítja a kamerát, és elhelyez egy tengely segéd objektumot a színtérben.

Hozzunk létre egy új geometriát.

var geometry = new THREE.Geometry();

Adjuk hozzá a csúcspontokat. Mivel a háromszögek közös csúcspontokon osztoznak, 5 darabot elég megadni.

geometry.vertices.push(
        new THREE.Vector3( -5.0, 5.0, 0.0 ),
        new THREE.Vector3( -2.5, 0.0, 0.0 ),
        new THREE.Vector3(  0.0, 5.0, 0.0 ),
        new THREE.Vector3(  2.5, 0.0, 0.0 ),
        new THREE.Vector3(  5.0, 5.0, 0.0 )
);

Adjuk meg a lapok tömbjét. Három ilyen lesz. Az indexelés 0-tól indul!

geometry.faces.push( new THREE.Face3( 0, 1, 2 ) );
geometry.faces.push( new THREE.Face3( 1, 3, 2 ) );
geometry.faces.push( new THREE.Face3( 2, 3, 4 ) );

Szükség lesz egy anyagra is.

var material = new THREE.MeshBasicMaterial( { color: 0xffff00, wireframe: false } );

Ezután jöhet a háromszögháló létrehozása és színtérhez adása.

var poly = new THREE.Mesh( geometry, material );
scene.add( poly );

Megjegyzés

A trapézt természetesen két háromszögből is összerakhatjuk: (0,1,4), (1,3,4); nincs feltétlenül szükség a 2 indexű csúcspontra.

Síkidom előlap és hátlap

Az OpenGL/WebGL/Three.js modellezés kapcsán fontos megértenünk a síkidom előlapok és hátlapok koncepcióját.

Próbáljuk ki a következőket az előző példaprogram kapcsán.

Mozgassuk úgy a kamerát az egérrel, hogy a trapéz "túlsó" oldalát lássuk. A háromszögek el fognak tűnni!
Módosítsunk a lapok indexsorrendjén a forráskódban. Például a második lap esetén az ( 1, 3, 2 ) sorrendet cseréljük le a logikusabbnak látszó ( 1, 2, 3 )-ra. A középső háromszög szemből nem jelenik meg, a túlsó oldalról viszont látszik, ahol a másik kettő nem!

A jelenség oka, hogy a modellezéskor alapértelmezésként a síkidomoknak csak az előlapja jelenik meg! Gondoljunk bele, ez logikus zárt felszínek "kívülről" történő megjelenítésekor, mivel a hátlapok biztosan nem látszanak a kamerából. Problémát jelent viszont nyílt felszínek, vagy sík geometriák esetén.

Hogyan adhatjuk meg, melyik legyen az előlap?

Ezt a lapok létrehozásakor az indexek sorrendje határozza meg. Az az előlap, amely esetén a kamerából nézve a csúcspontok megadási sorrendje ellentétes az óra járásával.

Hogyan jeleníthető meg mégis a hátlap is?

Az anyagnál a side attribútum értéket kell állítani, ahogyan korábban láttuk.