Elméleti áttekintés

Hisztogram

A hisztogram egy statisztika a vizsgált képen található intenzitások gyakoriságáról. A hisztogram vízszintes tengelyén az intenzitás értékékek tartományát, a függőleges tengelyen pedig az egyes intenzitások gyakoriságát adjuk meg.

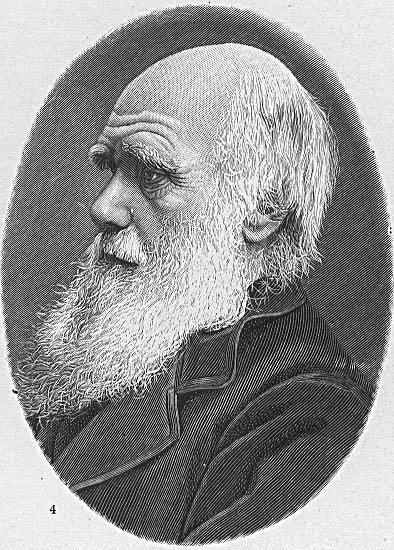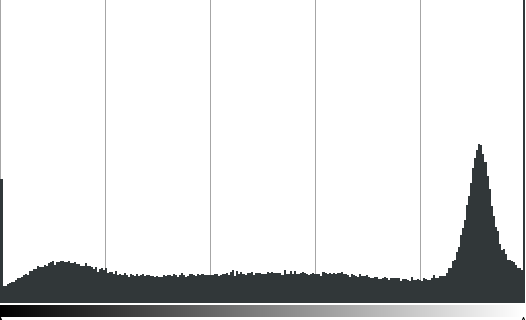Egy szürkeárnyalatos kép és hisztogramja

A hisztogram nem tárol tartalmi információt a képről, így magából a hisztogram nem tudunk arra vonatkozó következtetést levonni, mi látható a képen. Két különböző képnek is lehet ugyanolyan hisztogramja.

Habár tartalmi információt nem tudunk meg a hisztogramból, az intenzitások gyakorisága sok alkalmazásban hasznos lehet számunkra. Például küszöbölés esetén a hisztogram információt nyújt arról, hogy hogyan válasszuk meg a küszöbértéket. A fotózásban utómunkálataiban és a kép kontrasztosításában is jelentős segítséget nyújt.

Hisztogram széthúzás

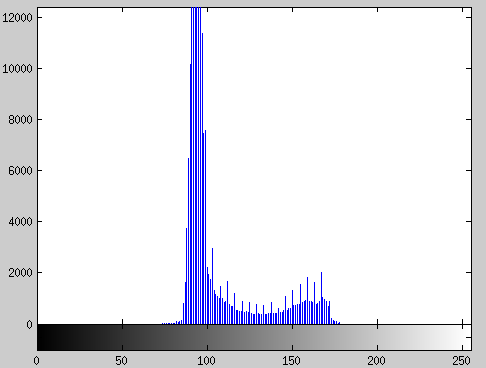
A hisztogram széthúzás célja, hogy a képen található iintezitások tartományát széthúzzuk az ábrázolható legnagyobb intenzitástartományra. Jelölje L-1 a képen ábrázolható legnagyobb intenzitást, továbbá jelölje min és max rendre a képen található legkisebb és legnagyobb intenzitást.

A hisztogram széthúzás művelete ekkor minden i intenzitásra a képen:

s = (L-1)(i-min) / (max - min),

ahol s az új intenzitás érték.

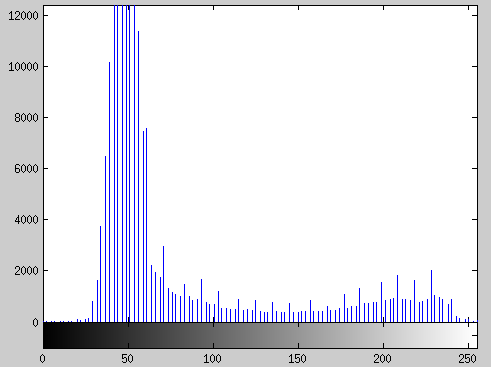Eredeti kép	A hisztogram széthúzás eredménye

Hisztogram kiegyenlítés

 A hisztogram kiegyenlítés célja, hogy kép intenzitásait úgy transzformálja, hogy az eredmény kép hisztogramja közel konstans legyen.

Határozzuk meg minden r intenzitáshoz az előfordulásának valószínűségét.
     p(r) = n_r / n,
ahol n_r az r intenzitás száma a képen, n pedig a kép pontjainak a száma.

Számoljuk ki az akkumulált hisztogramot minden r intenzitáshoz:
     h(r) = p(0) + ... + p(r)

Az r intenzitáshoz tartozó új s intenzitást úgy kapjuk, hogy az r intenzitáshoz tartozó akkumulált hisztogramot beszorozzuk az ábrázolható legnagyobb intenzitás értékkel.
     s = (L-1) * h(r)

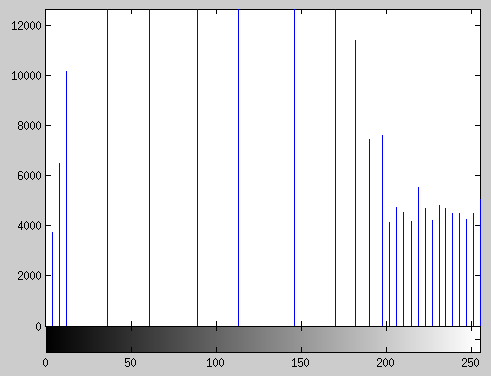Eredeti kép és hisztogramja	A kiegyenlített kép és hisztogramja